从《星汉灿烂》的数学题谈起
追剧刷题
七年级学生Shirley喜欢追剧,追完《梦华录》,又追《星汉灿烂》。当她追到《星汉灿烂》第六集:
上元节到来,街上到处张灯结彩。程家上下全家出游,程少商来到了田家酒楼外面,楼外挂着许多灯谜,袁慎正在楼里解谜,引来百姓们在楼下聚集。
何昭君在楼垚的陪同下来看热闹,撞了程少商一下,楼垚数落何昭君走路明明可以小心翼翼,却故意撞旁人。
田掌柜数落袁慎解谜太厉害了,导致楼下的灯笼越来越少,让百姓们想参与也没机会了。袁慎决定主动帮田掌柜出一题,让百姓们猜酒楼里面的水井深度。
程少商拿着酒楼给的尺子,算出了水井深度。
答对灯笼上的谜题可得千里醉一坛
女主程少商是怎样算出来的呢?解释一下,请看下图:
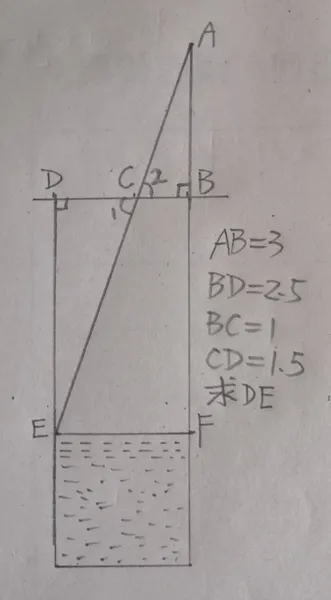
程少商的解答图
“井径二尺五,”指井的直径BD=2.5;“立三尺木于井上,”指AB垂直于BD,垂足是B,AB=3;“从木末望水岸,”指EF是井水的水平面,连接AE,交BD于C;“入径一尺,”指BC=1;“井口至水的深度是,”指DE的线段长度;“四尺半。”指所求答案是DE=4.5。
解题思路是相似三角形对应线段成比例,列比例式,知三求一,解比例式就得到答案。
根据程少商的解答图,Rt△ABC和Rt△CDE,∵∠1=∠2(对顶角相等),
∴ △ABC∽△CDE,
∴ AB:DE=BC:CD,
即 3:DE=1:1.5,
∴ DE=3×1.5÷1=4.5
单位是尺,一尺是多少厘米呢?
大家可以到评论区点击链接,跳转阅读。
古代数学中的规矩
有句古话叫“不以规矩,不成方圆”。现代人习惯把“规矩”放在一起作为一个词语,但在古代,规是规,矩是矩,它们分别是古人用来测量和画图的两种工具:“矩”是一种标有刻度的折成直角的曲尺,而“规”是专门用来画圆的圆规。
汉代以前的矩,曲尺的两臂是等长的,并且没有刻度;战国时期的矩,专门用来画直角;汉代以后的矩,曲尺的两臂一长一短,并且有了刻度,这时候的矩才演变成了几何测算工具。矩尺的两臂长短不同,更方便持握操作和查读数据。
古希腊的尺规作图和规矩作图大不一样。尺规作图是没有刻度的直尺,只能作直线,不能度量线段。而规矩的矩是曲尺,形状像L形,相当于两把有刻度的直尺成90°固定连接,可以测量线段,可以画直角。
古希腊搞的是理论数学,我国古代是应用数学高度发达。假如古希腊数学家见到中国古代的规矩,会惊呼中国人不讲武德。
确实是不讲武德。尺规作图可以解决特殊的三等分角作图,但是对任意角无能为力。而木工师傅的曲尺,古代的矩却可以轻轻松松解决三等分角的问题。
尺规作图不可能三等分任意角
矩可以三等分任意角
古代的规矩是怎样的呢?请看下图:
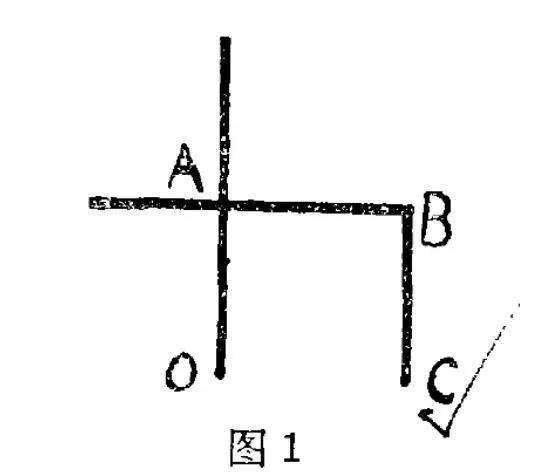
矩
规
这是规,由杆OA和矩ABC两个零件构成,可以环矩以为圆。
古代的矩很实用很方便,两臂有刻度,曲尺形方便画直角,作垂线。
古代数学家如何测量?
电视剧的题目太简单,不过瘾,请看《海岛算经》中的重差术。
《海岛算经》是魏晋时期刘徽所著的一部测量数学著作。也是中国学者编撰的最早一部测量数学著作,亦为地图学提供了数学基础。
《海岛算经》由刘徽于三国魏景元四年(公元263年)所撰,本为《九章算术注》之第十卷,题为《重差》。唐初开始单行,体例亦是以应用问题集的形式。
《海岛算经》共九问。都是用表尺重复从不同位置测望,取测量所得的差数,进行计算从而求得山高或谷深,这就是刘徽的重差术。《海岛算经》中,从题目文字可知所有计算都是用筹算进行的。“为实”指作为一个分数的分子,“为法”指作为分数的分母。所用的长度单位有里、丈、步、尺、寸;1里=180丈=1800尺;1丈=10尺:1步=6尺。
题目呈现
(1)今有望海岛,立两表齐高三丈,前后相去千步,令后表与前表参相直。从前表却行一百二十三步,人目着地取望岛峰,与表末参合。从后表却行一百二十七步,人目着地取望岛峰,亦与表末参合。问岛高及去表各几何?答曰:岛高四里五十五步;去表一百二里一百五十步。
却:后退。
[翻译:假设测量海岛,立两根表高均为3丈,前后相距1000步,令后表与前表在同一直线上,从前表退行123步,人目著地观测到岛峰,从后表退行127步,人目著地观测到岛峰,问岛高多少?岛与前表相距多远?
术曰:以表高乘表间为实;相多为法,除之。所得加表高,即得岛高。求前表去岛远近者:以前表却行乘表间为实;相多为法。除之,得岛去表数。
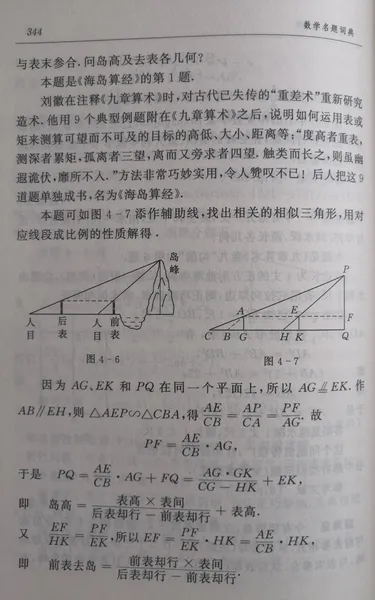
计算过程请看下图。
望清渊这道题难度比电视剧大得多,也是刘徽的得意之作。使用的测量工具是矩。
答案解析由南京师大数学系毕业的眭秋生撰写,并收录于江苏教育出版社的《数学名题词典》page343~345。
后辈的数学家在刘徽的基础上继续发展,应该有三角函数及三角学的诞生。但是没有,历史和中国人开了一个玩笑。
同样,古希腊数学虽然成就辉煌,但是没有函数。历史在静静等待近代西方数学的爆发。