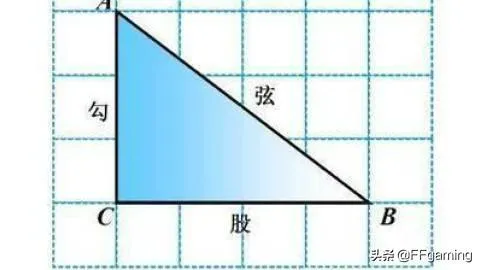
勾股定理常用公式,勾股定理怎么计算？
勾股定理公式
1、基本公式
在平面上的一个直角三角形中，两个直角边边长的平方加起来等于斜边长的平方。如果设直角三角形的两条直角边长度分别是a和b，斜边长度是c，那么勾股定理的公式为a+b=c。
2、完全公式
a=m，b=(m/k-k)/2，c=(m/k+k)/2其中m≥3
(1)当m确定为任意一个≥3的奇数时，k={1，m的所有小于m的因子}
(2)当m确定为任意一个≥4的偶数时，k={m/2的所有小于m的偶数因子}
3、常用公式
（1）(3,4,5),(6,8,10)……3n,4n,5n(n是正整数)。
（2）(5,12,13),(7,24,25),(9,40,41)……2n+1,2n+2n,2n+2n+1(n是正整数)。
（3）(8,15,17),(12,35,37)……2*(n+1),[2(n+1)]-1,[2(n+1)]+1(n是正整数)。
（4）m-n,2mn,m+n(m、n均是正整数,m>n)。
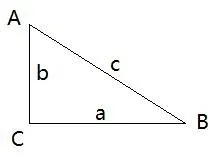
勾股定理怎么计算？
非常的简单直接来公式：a+b=c，其中a、b、c分别代表三角形的三个边长，只需要知道其中两个边长，或者知道三者的其他内在关系根据这个公式就可以计算出剩余的未知边长。
勾股定理：在任何一个直角du三角形中，两条直角边的平方之和一定等于斜边的平方。这个定理在中国又称为“商高定理”，在外国称为“毕达哥拉斯定理”。
勾股定理（又称商高定理，毕达哥拉斯定理）是一个基本的几何定理，早在中国商代就由商高发现。据说毕达高拉斯发现了这个定后，即斩了百头牛作庆祝，因此又称“百牛定理”。
勾股定理是几何数学中的基础，内容本身基本完全没难度，这个作为一个学科基础在后续的复杂研究中起到了关键性作用，希望这些内容大家在阅读之后能自己进行一定的实践，相信大家一定能快速的掌握。以上就是全部内容。
相关推荐
-
《热辣滚烫》票房超31.14亿 有望进入中国
《热辣滚烫》票房超31.14亿 有望进入中国影史前15位，趋势，专业版，热辣，票房，进入中国，史前，据灯塔专业版，截至2月23日0时，影片《热辣滚烫》票房超31.14亿，超过影片《八佰》，进入中国影史票房前17位！第16位是《我和我的祖国》（31.70亿），第15位是《美人鱼》（33.93亿），照此趋势，《热辣滚烫》进入TOP15有很大可能。本片由贾玲执导、贾玲、雷佳音领衔主演，张小斐、沙溢等友情出演。在收获高票房同时，豆瓣评分...
-
《熊出没·逆转时空》票房超16.65亿 进入
《熊出没·逆转时空》票房超16.65亿 进入中国动画电影TOP3，熊出没，逆转，院线，趋势，十周年，特效，据灯塔专业版，影片《熊出没·逆转时空》2月22日票房达3513.6万，超过2月21日3481.7万，实现票房逆跌！本片当前总票房已超过16.65亿，进入中国影史动画电影票房前三位。排名前两位的是《哪吒之魔童降世》（50.36亿元）和《长安三万里》（18.24亿元）。从目前的趋势来看，《熊出没·...
-
《家庭简史》柏林电影节首映：展现中国家庭
《家庭简史》柏林电影节首映：展现中国家庭的幽微内核，中国，内核，视角，项目，有限公司，单元，柏林当地时间2月21日，入围今年第74届柏林电影节全景单元的中国影片《家庭简史》举行了欧洲首映礼。该片由杭州凯阔文化传播有限公司、霍尔果斯万年影业有限公司、北京万年奈思文化传媒有限公司等出品，也是一部浙江出品的艺术电影。《家庭简史》由林见捷编剧、执导，祖峰、郭柯宇、孙浠伦、林沐然主演，楼莹、郑玥、王衣文担任制片人。讲述了涂伟一家看似波澜不惊的...
-
《熊出没10》票房超《姜子牙》 进入中国
《熊出没10》票房超《姜子牙》 进入中国影史前三，熊出没，姜子牙，动画，连续，逆转，年在，据灯塔专业版数据显示，2024春节档动画《熊出没·逆转时空》上映第13天，累计总票房超16.64亿，超过《姜子牙》（16.03亿元）进入中国影史动画电影票房榜前三。影片2月22日票房达3513.3万，超过2月21日3481.7万，再次实现票房逆跌。该片是“熊出没”系列动画电影连续第十年在春节档与观众见面，自...
-
《熊出没·逆转时空》票房排名中国动画影
《熊出没·逆转时空》票房排名中国动画影史第二位，熊出没，逆转，动画，中国，期待，特效，据灯塔专业版，截至2月25日，影片《熊出没·逆转时空》票房超18.26亿，超过《长安三万里》进入中国影史动画电影票房TOP2！对于《熊出没·逆转时空》，此前有电影机构给出了20亿的预测票房。据了解，《熊出没·逆转时空》是《熊出没》系列的第10部院线大电影，也是该系列的十周年纪念之作，因此备受期待。《...
-
2月中国电影票房破百亿元 其中《热辣滚烫
2月中国电影票房破百亿元 其中《热辣滚烫》27亿元，中国，数据，收入，突破，假期，显示，据香港《南华早报》网站2月24日报道，根据最新的统计，在春节八天假期里，人们大量涌入电影院观影。在此推动下，中国2月的电影票房收入已超过100亿元人民币。报道称，根据国家电影局、票务服务公司猫眼和电影数据平台灯塔专业版的数据，仅在2月10日至17日期间，中国影院就售出80亿元人民币的电影票，其中喜剧电影《热辣滚烫》在此期间的票房收入为27亿元。...
-
《功夫熊猫4》举行中国首映礼 黄渤杨幂蒋
《功夫熊猫4》举行中国首映礼 黄渤杨幂蒋欣亮相，功夫熊猫，中国，角色，魅影，元素，新手，3月14日，即将于3月22日全国上映的动画电影《功夫熊猫4》在北京环球影城举行了盛大的中国首映礼。作为该动画电影配音的明星演员，黄渤、杨幂、蒋欣在映后悉数亮相，并与现场的观众进行了简单的交流。黄渤此次为“功夫熊猫”阿宝献声，现场直言终于遇到它了。《功夫熊猫1》到《功夫熊猫4》跨越了16年，“我在第一部看的时候就...
-
外国IP中国改编 《大唐狄公案》如何突破
外国IP中国改编 《大唐狄公案》如何突破重围实现口碑逆袭，角色，中国，突破，期待，演绎，分化，近期备受期待的《大唐狄公案》开播了，目前已经播了18集，口碑争议挺多的。这部承载着观众高度期待的历史悬疑大剧，是否还有可能实现口碑逆转，周一围能否重现“狄仁杰”系列的魅力？历史上的狄仁杰，是中国唐朝时期的一位著名政治家，他的事迹主要记载于《旧唐书》和《新唐书》中。鉴于这个人物的影响力以及影视改编的传统，《大唐狄公...
-
《中国车手周冠宇》定档 讲述中国首位F1
《中国车手周冠宇》定档 讲述中国首位F1车手的成长故事，中国，赛车，比赛，正式，速度，车手，纪实电影《中国车手周冠宇》定档4月19日，影片于3月19日发布“极限突围”版定档预告及同名定档海报。该片记录了中国首位F1车手周冠宇的成长历程，将带领观众走近并见证他从追寻赛车梦想的少年成长为F1正式车手的艰辛历程，让观众从不同角度深入了解这位车手。同时，这也是对F1中国大奖赛举办20周年的献礼。纪实电影《中国车手周冠...
-
外国IP中国改编，《大唐狄公案》如何突破重
外国IP中国改编，《大唐狄公案》如何突破重围实现口碑逆袭，角色，中国，突破，期待，演绎，分化，近期备受期待的《大唐狄公案》开播了，目前已经播了18集，口碑争议挺多的。这部承载着观众高度期待的历史悬疑大剧，是否还有可能实现口碑逆转，周一围能否重现“狄仁杰”系列的魅力？历史上的狄仁杰，是中国唐朝时期的一位著名政治家，他的事迹主要记载于《旧唐书》和《新唐书》中。鉴于这个人物的影响力以及影视改编的传统，《大唐狄公...
-
李胜利事件涉及到的中国艺人 李胜利n号房
李胜利事件涉及到的中国艺人 李胜利n号房 胜利事件中国艺人，事件，中国，店里，大陆，艺人，业务，升级，媒体， 李胜利事件涉及到的中国艺人 李胜利n号房 胜利事件中国艺人。韩国男子团体中李胜利是最年轻的成员，除了他的主要业务—偶像外，还开始了边线—老鸨。原因是一个男英雄拯救了美女。在李胜利的店里，他救出了一位向他求助的漂亮女子，但他遭到了店员的殴打。还污蔑说他是在店里轻薄女性客人。 在1月份，李胜利所经营夜店也是被曝出了暴...
-
《青春18×2》3月14日中国台湾上映 许光
《青春18×2》3月14日中国台湾上映 许光汉同框道枝骏佑，日本，旅程，清原，合拍，剧情，主题，2月18日，合拍电影《青春18×2 通往有你的旅程》发布“18年前的台湾”和“现在的日本”两组主题剧照，解锁更多新画面，其中主演许光汉和共演道枝骏佑的同框合照引爆话题。有着“想见你2.0版”之称的《青春18×2》讲述了18年前，高中生吉米（许光...
-
2月电影票房破110亿 排名中国影史单月票
2月电影票房破110亿 进入中国影史单月票房TOP3，中国，逆转，熊出没，数据，专业版，捉妖记，据灯塔专业版数据，截至2月27日18时53分，2024年2月总票房（含预售）破110亿。本月票房也成为当前中国影史单月票房第三位，这也是中国影史第6次单月票房破100亿。据了解，中国电影单月票房首破100亿是2018年2月，当年春节档上映的影片包括《唐人街探案2》、《红海行动》、《捉妖记2》、《熊出没之变形记》、《西游记女儿国》等多部新片。今...
-
五岳是指哪五座山?,中国五岳是指哪五座山
五岳是指哪五座山?,中国五岳是指哪五座山？，中国，海拔，泰安市，南岳衡山，帝王，名山，东岳，城南，中国五岳分别是：东岳泰山、西岳华山、南岳衡山、北岳恒山、中岳嵩山。五岳曾是封建帝王仰天功之巍巍而封禅祭祀的地方，更是封建帝王受命于天、定鼎中原的象征。1.东岳泰山：泰山海拔1545米，位于山东省泰安市泰山区，隶属于泰安市，绵亘于泰安、济南、淄博三市之间，总面积24200公顷。主峰玉皇顶海拔1545米，气势雄伟磅礴，有“五岳之首”、“五岳之长”、五岳之尊、“天下第一山”...
-
张元英用中文回复来自中国的粉丝 还微笑
，组合，中国，中文，比心，发行，正式，3月15日，张元英出席某活动并和粉丝群体打招呼，当张元英用英语询问粉丝来自哪个国家，并得知对方是中国粉丝后，立刻用中文说谢谢，还微笑比心，可以说是十分宠粉。对此，有不少网友表示张元英面对一群亚洲面孔的粉丝时，愿意询问对方具体国籍并作出对应回复，十分难得。张员瑛，2004年8月出生于韩国首尔特别市，女子演唱组合IVE成员。 2018年6月，参加韩国选秀节目《Produce 48》，最终在节目中获得第一...
-
《数码宝贝02：最初的召唤》定档 中国内地4
《数码宝贝02：最初的召唤》定档 中国内地4月20日上映，数码宝贝，召唤，接触，数码世界，事件，日内，《数码宝贝》动画开播25周年之际，迎来全新剧场版《数码宝贝02：最初的召唤》，影片定档4月20日内地上映。本部剧场版将围绕“光丘事件”后，首个与数码宝贝接触的人类大和田类与他的数码宝贝乌科兽之间发生的故事展开。数码世界史上最大的危机降临，被选召的孩子们将再次出动，开启新一轮的冒险旅程。在最新发布的预告中，跟随...